Illustration : Jeremiah Horrocks observant le transit de Vénus de décembre 1639, Eyre Crowe 1891.

La loi erronée de Remus Quietanus,  ou Horrocks’s bogus law.

Dans un article récent [1], nous mettions le doigt sur un point de désaccord entre l’astronome Johannes Kepler, acteur majeur de la révolution copernicienne et notre astronome rouffachois Johannes Remus Quietanus. Il s’agit de l’évaluation de la distance de la Terre au Soleil et partant, de la dimension du système solaire tout entier que Quietanus imaginait quatre fois plus grand que son ami Kepler. En effet Kepler estimait la distance de la Terre au Soleil à 3400 fois le rayon de la Terre, alors que selon Quietanus, cette distance était de 14 000 rayons environ.

On peut se demander sur quels fondements l’un et l’autre s’appuyaient pour proposer ces valeurs, c’est ce que nous exposerons dans la suite, mais nous remarquerons d’abord que Quietanus n’était pas le seul à proposer ses 14000 RT, puisqu’en 1639 l’anglais Jeremiah Horrocks donnait cette même valeur sans rien connaître, apparemment, de l’opinion de Quietanus sur ce sujet.

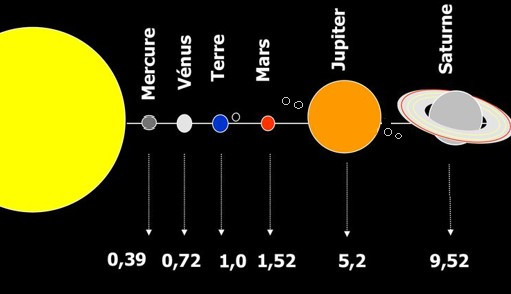
Dans la correspondance de Quietanus avec Kepler, il a souvent été question de la dimension du système solaire et des distances interplanétaires. En 1619, Kepler avait publié ses Harmonices Mundi, un ouvrage majeur ou il énonçait sa troisième loi,  T²= D³, qui établit une relation entre les périodes de révolution des planètes et leurs distances au Soleil. Cette égalité simple est vraie pour toutes les planètes si on exprime leurs périodes de révolution en années et leurs distances au Soleil en unités astronomiques  où, par définition, 1 UA est la distance de la Terre au Soleil.

Quietanus n’a jamais contesté cette découverte du maître et au contraire, il en était admiratif. Ainsi, l’on pouvait calculer les distances des planètes au Soleil, obtenant les valeurs suivantes [2] :

Les deux astronomes étaient tout à fait d’accord sur ces valeurs, exprimées en unités astronomiques, mais leur désaccord portait sur la valeur de cette unité, 3400 fois le rayon de la Terre pour Kepler ou 14 000 fois le rayon de la Terre pour Quietanus. 

Le transit de Mercure du 7 novembre 1631

Pour comprendre cette différence d’évaluation de l’unité astronomique, il nous faut relire le compte-rendu de l’observation du transit de Mercure de 1631. En 1627, Kepler avait calculé qu’à l’automne 1631, se produiraient des transits planétaires, c'est-à-dire des alignements parfaits entre le Soleil, Mercure et la Terre en novembre et entre le Soleil, Vénus et la Terre en décembre 1631. Ces phénomènes relativement rares et indécelables à l’œil nu n’avaient jamais été observés de mémoire d’astronome et Kepler eut la bonne idée de faire part de sa prévision à ses collègues. Ainsi, il publia en 1629 son Admonitio ad Astronomos, avertissement aux astronomes. Bien lui en prit, puisque son destin ne lui permit pas d’observer lui-même ces transits : il mourut en novembre 1630.

Les quatre chanceux qui purent observer le transit de Mercure du 7 novembre 1631 furent tous surpris de voir la planète aussi petite devant le disque solaire. Voici le compte-rendu du rouffachois Remus Quietanus adressé à l'archiduc Léopold [3] :  

Le 7 novembre à 9h 42’ 30’’du matin, j’ai aperçu subitement une petite tache à peine le tiers d’un scrupule au–delà du centre du Soleil, de couleur presque noire d’acier, très différente des autres taches. Son diamètre était d’environ 18’’ et déjà à 11 heures AM, elle avait dépassé le quart depuis l’observation précédente de Mercure. Par le calcul j’ai donc déduit que le début de son incursion a eu lieu à Rouffach la nuit à 5h35 ¾ après minuit à la latitude 0°0’0’’, le milieu de la rencontre à 8h 10’AM.

Cette petite taille de Mercure (18 secondes d’arc) par rapport à la taille du Soleil (30 minutes) confortait Remus Quietanus dans l’idée que la distance de la Terre au Soleil devait être grande, ses explications sont un peu délayées :

Dès lors, mon opinion au sujet des diamètres des corps célestes est confortée, à savoir celui de Saturne est presque 10 fois celui de la Terre, 100 fois en superficie (du disque) et 1000 fois en volume. Pour Jupiter, c’est 5 fois, 25 fois et 125 fois en volume, pour Mars 1,5 etc. quant à Vénus et Mercure, ils n’égalent pas le volume de la Terre, car Vénus est à peine le tiers et Mercure le douzième [4]. Le Soleil, lui, occupe 60 diamètres terrestres, son disque 3600 et son volume 216000 (le volume de la Terre), de sorte que l’espace occupé par le Soleil égale précisément toute la sphère de la course de la Lune  autour de la Terre, ce qui chez Ptolémée n’était que de 166 fois.
La proportion des sphères est donc exactement la même, pour moi, que celle des diamètres des globes des planètes si quelqu’un les voyait toutes alignées à partir du centre du Soleil, il les verrait toutes sous le même angle, à savoir 30 secondes [5].

Pour chaque planète, il parle de la superficie et du volume : ce sont là des considérations inutiles pour sa conclusion. Mais la dernière phrase nous livre la base de son calcul : il y formule une hypothèse que nous appellerons Loi de Quietanus.

 La « Loi de Quietanus »

Remus Quietanus postule que les diamètres des planètes sont proportionnels à leur éloignement du Soleil : « Si quelqu’un les voyait toutes alignées à partir du centre du Soleil, il les verrait toutes sous le même angle ».

Ce postulat est faux [6], pourtant il n’est pas stupide : il se trouve que vus depuis la Terre, la Lune et le Soleil présentent des disques quasiment superposables, c’est ce qui se passe lorsque lors d’une éclipse de Soleil, le disque de la Lune cache quasi exactement celui du Soleil. On peut juste se dire que c’est là un hasard extraordinaire… alors pourquoi le Créateur n’aurait-il pas répété ce hasard pour donner aux hommes une clé qui leur permette de décrypter son Œuvre ?

Quoiqu’il en soit, si cet angle est de 30 secondes, comme l’affirme Quietanus, on obtient alors une unité astronomique de 1/sin(15’’), ce qui donne 13 751 fois le rayon de la Terre. Qu’en est-il alors du calcul de Kepler ?

Le postulat de Kepler

C’est encore le compte-rendu de Quietanus qui nous permettra de comprendre comment Kepler a donné son estimation de la distance Terre-Soleil :

Remus ajoute ensuite : Kepler considère le diamètre de l’orbite lunaire comme moyenne proportionnelle entre le Soleil et la Lune, c'est-à-dire le diamètre de la Terre est au diamètre de l’orbite lunaire ce que le diamètre de l’orbite lunaire est au diamètre de l’orbite de la Terre [7].

Moi, je dirais plutôt : le diamètre de la Lune est au diamètre de l’orbite lunaire ce que le diamètre de l’orbite lunaire est au diamètre de l’orbite terrestre. Voici ce que Remus Quietanus a écrit au Sérénissime Léopold.

En notant r_T  le rayon de la Terre, cette hypothèse de Kepler se traduit par TL² = TS x r_T
On admet de nos jours que la distance moyenne Terre-Lune  est voisine de 60 r_T , le calcul de Kepler donnerait alors TS = 3600 r_T . Dans ses commentaires de la correspondance de Kepler [8], Max Caspar écrit que pour Kepler, TS = cotg (1’) r_T , soit 3437 r_T  , il n’explique pas l’obtention de cette valeur.

Un Monde plus grand

Dès 1629, Kepler s’était ému de cette inflation des valeurs estimées de l’unité astronomique : « Hipparque (ou Aristarque) plaçait le Soleil dans le ciel à une hauteur de 1200 Rayons terrestres. J’en ai fait une hauteur de 3400 Rayons terrestres, mais lui (Quietanus), il en rajoute encore dix-mille ce qui lui donne 14 000 rayons terrestres [9] » !
C’étaient les dimensions de l’univers tout entier qu’il fallait alors reconsidérer, et pourtant, il n’imaginait pas que même le monde selon Quietanus était encore trop petit.

En décembre 1631, les conditions météorologiques n’ont pas permis aux astronomes avertis d’observer le transit de Vénus. Mais l’anglais Jeremiah Horrocks calcula que Vénus devrait repasser devant le Soleil 8 ans plus tard, le 4 décembre 1639, ce qui lui permit d’être le premier observateur de ce phénomène [10]. Comme Quietanus voyant Mercure, Horrocks s’étonna de la taille de Vénus, plus petite que prévue et il fit un calcul analogue  à celui du rouffachois, avec l’hypothèse qu’un angle de 28’’ placé au centre du Soleil intercepterait toutes les planètes. Il trouva ainsi que 1 UA= 14 733 rayons terrestres.
Un article paru en 2005 dans Astronomy & Geophysics sous le titre « Horocks’s bogus law » relate ce calcul de Jeremiah Horrocks et donne à penser que l’anglais ne connaissait pas le résultat de Quietanus. Il est alors étonnant qu’il ait fait le même postulat erroné, cette idée était-elle donc dans l’air du temps ?

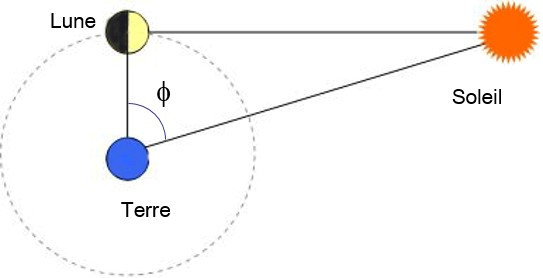
En 1635 [11], l’astronome flamand Godefroy Wendelin essaya de reprendre la démarche d’Aristarque de Samos pour recalculer l’unité astronomique. La justesse théorique de cette méthode est indubitable, mais elle est très imprécise puisqu’il faudrait savoir  pointer exactement l’instant où la Lune est à moitié éclairée (dichotomie de la Lune). Alors que le grec donnait entre 380 et 1520 rayons terrestres, Wendelin en fit 14 000. Curieusement son résultat était en accord avec celui de Quietanus… oserions-nous imaginer qu’il  en avait une idée préconçue ?

Illustration du Calcul d’Aristarque et Wendelin :

En réalité, l’angle φ (Phi) est proche de 90° et la moindre augmentation accroît considérablement l'hypoténuse, d’où l’imprécision  inhérente de la méthode.

Dès la fin du XVIIe siècle, le génie inventif des astronomes leur fit imaginer d’autres stratégies pour pouvoir calculer l’unité astronomique de façon plus sûre, les uns tablaient sur des observations simultanées d’un transit de Vénus tandis que d’autres utilisaient l’excentricité de l’orbite de Mars et des observations simultanées de son passage à l’opposition [12]. En 1659, Christian Huygens estimait l’unité astronomique à 24 000 RT, tandis qu’en 1672, Cassini et Richer la ramenaient à 21 700 RT. La valeur admise en 2020 est de 23 455 RT.

On aurait tendance à laisser Kepler à ses états d’âme ; ce serait injuste ! Certes, il s’était trompé, mais il a  su faire preuve d’humilité et mettre en doute son résultat. Il faut aussi rappeler que c’est lui, Kepler qui patiemment a étudié la trajectoire de Mars pour comprendre que c’est une ellipse avant de calculer son excentricité, trouvant ainsi la clé de la mécanique céleste. Et c’est encore Kepler, le premier qui a su prévoir les dates des transits des planètes, rendant ainsi possibles les mesures effectuées par ses successeurs. Il convient donc une fois de plus de lui rendre hommage et de reconnaître qu’il fut l’initiateur de cette quête scientifique.
Quant à Remus Quietanus, dans cette controverse il a osé imaginer un monde 4 fois plus grand, conférant au Soleil et à son système planétaire un ordre de grandeur plus juste. Rien qu’à ce titre, on pourrait souhaiter que son nom figure sur les tablettes.

Jacques Mertzeisen, avril 2020

Liens et bibliographie

David W. Hughes, Horrocks’s bogus law, Astronomy & Geophysics n°46, 2005.

Paul Courbon, Le transit de Vénus ou mesurer l’espace, XYZ n°148, 3^e trimestre 2016.

Georges  Paturel, La mesure de la distance de la Terre au Soleil, 2010.

Wikipédia, Unité astronomique.

1981. Misar, Petite histoire de la parallaxe du Soleil, Les cahiers de Clairaut n° 14, 1981.

S.J. Goldstein Jr, Christiaan Huygens’ measurement of the distance to the Sun, University of Virginia, 1985.

Notes: 

[1] Voir « De la Terre au Soleil », Jacques Mertzeisen sur Obermundat.

[2] NB : Ces valeurs sont données dans une lettre de Quietanus à Kepler de décembre 1628, elles sont presque  égales aux valeurs admises en 2020 (9,55 pour Saturne). Uranus et Neptune ne sont pas encore connues.

[3] Extrait du Liber Duodecimus de Historia Coelestis accessible en ligne à ETH-Zürich, pages 955 & 956.

[4] 1/16 serait plus juste.

[5] Dans le texte, on lit 30 minutes, mais c’est une faute d’imprimerie.

[6] En réalité, on verrait Jupiter sous un angle de 37’’, mais Mars sous un angle de seulement 6’’ et la Terre sous un angle de 17,5’’. Il est étonnant que  Quietanus n’ait pas vu que Mars est franchement trop petite. Saturne doit être considérée avec ses anneaux  y compris.

[7] Les deux phrases ne disent pas la même chose, il semble qu’il y ait une erreur typographique dans la première, la deuxième se traduit par (2r_T)/(2TL) = (2TL)/(2TS)

[8] Max Caspar, Johannes Kepler Gesammelte Werke, volume 18, commentaires de la lettre 1101, page 552.

[9] Lettre de Kepler à Wallenstein, voir Johannes Kepler Gesammelte Werke, volume 18, lettre 1101, page 292.

[10] Dans l’appendice de son discours astronomique et astrologique de 1642, Quietanus affirme qu’il avait également essayé d’observer ce transit de  décembre  1639, mais que les conditions météorologiques ne l’ont pas permis. Voir l’article sur Obermundat, dernier paragraphe.

[11] Date discutée : Sur la page Unité Astronomique de Wikipédia, on trouve 1635, sur Godefroy Wendelin, on trouve « vers 1630 »… David W. Hughes donne 1647. 

[12] Voir les documents Georges Paturel et K. Misar dans la bibliographie qui suit.