En ce mois de février 2023, nous nous réjouissons de la parution des Saisons d’Alsace n°95, un numéro spécialement consacré à l’Astronomie en Alsace. J’ai été contacté dès l’automne pour y rédiger un petit article sur notre astronome local. Comme j’avais déjà pu écrire dans le n°74 une présentation de la biographie de Remus Quietanus, médecin et astronome rouffachois, j’ai choisi de développer un point plus spécifique. Ce nouvel article revient donc sur la controverse qui opposait Kepler et Quietanus au sujet de la distance de la Terre au Soleil, une question déjà évoquée sur Obermundat[1].

En préparant cette publication pour « les Saisons », j’ai mené quelques recherches complémentaires qui m’ont permis de trouver la réponse à une question que je me posais depuis la lecture d’un article paru en 2005 dans une revue anglophone. C’est une petite avancée que je voudrais partager avec les lecteurs d’Obermundat.

Jacques Mertzeisen

Revenons d’abord sur cette controverse qui oppose Kepler à Remus Quietanus :

Johannes Kepler est l’un des astronomes les plus célèbres, il doit cette notoriété principalement à l’énoncé de trois lois qui décrivent le mouvement des planètes autour du Soleil. Les deux premières lois stipulent que les planètes ne décrivent pas des cercles, mais des ellipses autour du Soleil et que les mouvements des planètes sur ces trajectoires ne sont pas uniformes : les planètes ralentissent lorsqu’elles s’éloignent du Soleil jusqu’à atteindre l’aphélie, puis elles accélèrent en revenant plus près de Soleil jusqu’à leur passage au périhélie.

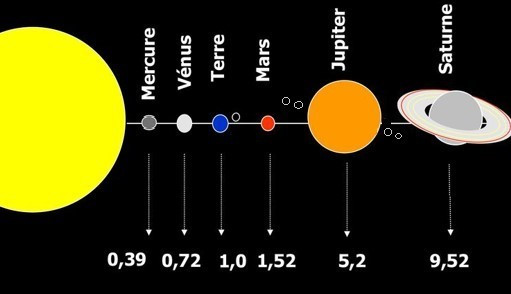
La troisième loi de Kepler donne une relation simple liant les distances des planètes au Soleil à leur période de révolution. Elle a été publiée en 1619, à une époque où Kepler et Remus Quietanus s’écrivaient régulièrement. Tous deux étaient parfaitement d’accord sur les distances des planètes au Soleil, calculées grâce à cette 3^e loi de Kepler, qui s’exprimaient en unités astronomiques où, par définition, 1 unité est la distance de la Terre au Soleil. (Voir schéma ci-dessous)

Mais ils étaient en grand désaccord sur la valeur de l’unité elle-même : Kepler l’estimait à environ 3400 fois le rayon de la Terre, tandis que pour Quietanus, c’était plutôt 14 000 fois ce rayon. Nous savons, de nos jours que cette distance fait environ 150 millions de kilomètres, soit 23 500 fois le rayon de la Terre.

En 2020, j’ai déjà présenté ce désaccord de nos deux astronomes sur Obermundat et expliqué que même si l’estimation de Remus Quietanus est meilleure que celle de Kepler, elle n’en repose pas moins sur un postulat erroné que j’ai appelé « postulat de Quietanus » :

«Si quelqu’un  voyait toutes les planètes alignées à partir du centre du Soleil, il les verrait toutes sous le même angle, à savoir trente secondes »

Je m’étonnais aussi que l’astronome anglais Jeremiah Horrocks, qui fut le premier à observer un transit de Vénus en décembre 1639, avait formulé le même postulat que Remus Quietanus pour en arriver à la même estimation de la distance de la Terre au Soleil. Un article publié en 2005 par David W Hughes dans la revue Astronomy & Geophysics[2] laissait entendre que Horrocks ne connaissait pas le compte-rendu de Quietanus de son observation du transit de Mercure de 1631 où il développe sa théorie. Cependant, comme le rouffachois, il avait lu un opuscule publié par Kepler en 1629 « Admonitio ad Astronomos » où Kepler annonçait les transits de Mercure et Vénus de 1631.

Entretemps, j’ai pu dénicher une version en ligne de cet avertissement de Kepler à l’adresse de ses collègues astronomes[3], malheureusement écrit en latin. À la page 10, Kepler fait clairement allusion au problème de la distance de la Terre au Soleil, et il mentionne nommément Remus Quietanus qui l’incite à reconsidérer la valeur de cette distance :

Extrait de l’Admonitio ad Astronomos, pages 10 et 11

Et de cette vraie méthode, qui pose comme fondement que la grandeur des corps planétaires est proportionnelle à leur distance au Soleil, est né le précepte 110, page 75 des Tables Rudolphines, tel qu'il est conseillé au Lecteur à la fin du précepte. Cependant, nous ne disposons pas de bases entièrement limpides. Car le diamètre du corps de Mars aurait dû dépasser 6 minutes lorsqu'il était le plus proche de la Terre dans le Verseau :  mais le télescope utilisé semble rejeter un tel diamètre, comparaison faite des diamètres de Mars et de Vénus dans le Capricorne en 1623.

Et ainsi moi-même, dans les Hyperaspistes de Tycho, j'ai indiqué que je devrais encore délibérer avec Galilée ; et ce même Johann Remus Quietanus, à l'avis duquel dans ledit Epitome p. 485 je m’étais rangé, maintenant il s’en détache ; et en attendant, en retenant en partie cette éventualité que, si les corps sont [plus ou]moins proportionnels aux intervalles, il rend du moins les diamètres de tous les six égaux entre eux, et du reste j’écarterais Mars dans la position d'Acronychus de la Terre jusqu'à n'en faire aucune apparence plus grande que celle dont le télescope atteste. Et avec ces principes, il en résulte que, tandis que j'avais récemment triplé l'ancienne distance entre le Soleil et la Terre, la mienne, à son tour, devait être quadruplée, et ainsi l'ancienne distance ptolémaïque devrait être multipliée par douze.[4]

Commentaires :

• Les Tables rudolphines, l’Epitome et les Hyperaspistes de Tycho Brahe sont des publications de Kepler.
• Ptolémée donnait une distance Terre-Soleil de 1200 rayons terrestres ; apparemment Quietanus avait déjà dû convaincre Kepler pour tripler cette estimation et maintenant il voulait encore la quadrupler.
• La proportionnalité évoquée par Kepler est le postulat de Quietanus évoqué plus haut et illustré par le dessin de l’article anglais.
• Mars en position d’Acronychus signifie Mars en opposition, plus simplement. Kepler pointe ici du doigt que Mars fait exception au postulat de Quietanus.

On retiendra de cet extrait que Kepler est perplexe mais qu’il ne rejette pas complètement l’avis de notre astronome rouffachois, laissant la question ouverte. Et, s’il évoque la question de la distance de la Terre au Soleil dans ce fascicule censé informer de transits planétaires à venir, c’est parce qu’il pense que l’observation de ces transits est une occasion de confirmer ou d’infirmer cette théorie de l’égalité des diamètres apparents des planètes vues depuis le Soleil qu’il attribue à Remus Quietanus. Kepler fait preuve ici d’une humilité qui ne fait que s’ajouter à sa grandeur d’âme.

À la lecture de ce passage de l’Admonitio on comprend mieux comment Quietanus et Horrocks en sont arrivés à la même estimation des dimensions du système solaire, l’un après son observation du transit de Mercure de 1631, l’autre après le transit de Vénus de 1639.

Jacques Mertzeisen, février 2023

Bibliographie :

• Une controverse opposait Kepler à l’astronome alsacien Remus Quietanus, Les Saisons d’Alsace n°95, pages 80 à 83.
• Obermundat, La loi erronée de Remus Quietanus, ou Horrocks's bogus law
• Obermundat, Johannes Remus Quietanus, astronome et médecin à Rouffach
• David W. Hughes, Horrocks’s bogus law, Astronomy & Geophysics n°46, 2005.
• Wikipédia, Unité astronomique; Jeremiah Horrocks.

 Notes :

[1] Voir De la Terre au Soleil ... - Obermundat et La loi erronée de Remus Quietanus, ou Horrocks's bogus law - Obermundat

[2] David W. Hughes, Horrocks’s bogus law, Astronomy & Geophysics n°46, 2005.

[3] University of Oklahoma, Galileo’s World, Johannes Kepler, Jacob Bartsch, Admonitio ad adtronomos, pages 10 et 11.

[4] Je remercie Jean Gemberle pour son aide à la traduction de ce passage.

Droit d'auteur et propriété intellectuelle

L'ensemble de ce site relève de la législation française et internationale sur le droit d'auteur et la propriété intellectuelle. Tous les droits de reproduction sont réservés. Toute utilisation d'informations provenant du site obermundat.org doit obligatoirement mentionner la source de l'information et l'adresse Internet du site obermundat.org doit impérativement figurer dans la référence.